Variationskoefficienten är ett statistiskt mått på fördelningen eller spridningen av data runt medelvärdet. Detta mått används för att analysera skillnaden i spridning i data i förhållande till medelvärdet. Variationskoefficienten härleds genom att dividera standardavvikelsen med medelvärdet.
Varning
Om medelvärdet för data är noll är det inte möjligt att beräkna varianskoefficienten. På liknande sätt, om data innehåller både positiva och negativa värden, är varianskoefficienten inte ett tillförlitligt statiskt mått. Varianskoefficient är ett tillförlitligt statiskt mått endast om data innehåller positiva värden.
Dricks
Variationskoefficient används för att kontrollera konsistensen av data eller provvärden i vetenskapliga experiment. Om variationskoefficienten är hög, visar den inkonsekvensen av data eller provvärden.
Steg 1
Identifiera den uppsättning tal för vilken variationskoefficienten ska beräknas. Ange uppgifterna på Excel-arket. Det här exemplet använder cellerna A2:A7, men din Excel-fil kan använda andra celler.
Dagens video
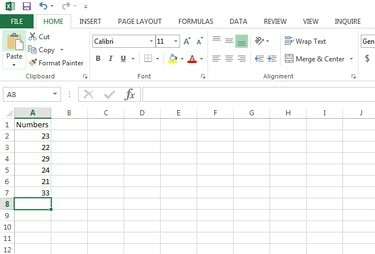
Microsoft Excel-datainmatning.
Bildkredit: Gurudev Ravindran
Steg 2
Använd funktionen Stdev (nummer1, [nummer2]...) att beräkna standardavvikelse i Microsoft Excel. Mata in formeln =Stdev (A2:A7) för det här exemplet -- men skriv in din faktiska cellanvändning i din Excel-fil -- i en tom cell och tryck Stiga på för att beräkna standardavvikelsen.
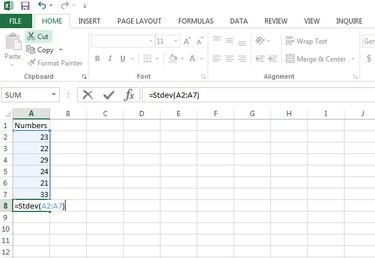
Beräkna standardavvikelsen.
Bildkredit: Gurudev Ravindran
Dricks
Varje formel i Microsoft Excel måste föregås av likhetstecknet.
Steg 3
Använd funktionen =Genomsnitt (nummer1, [nummer2],...) för att beräkna medelvärdet i Microsoft Excel.
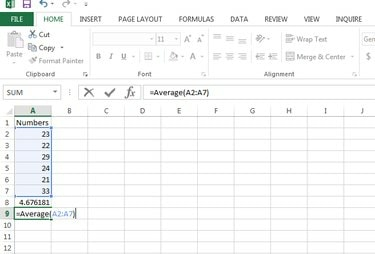
Beräkna medelvärdet.
Bildkredit: Gurudev Ravindran
Steg 4
För att hitta variationskoefficienten, mata in formeln =A8/A9 för detta exempel eller ditt faktiska intervall i en tom cell och tryck E**nter** för att beräkna varianskoefficienten.
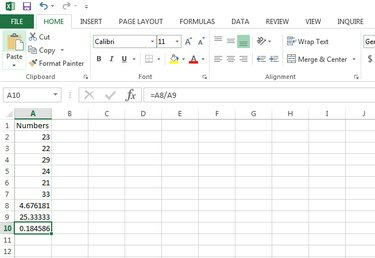
Beräkna varianskoefficienten.
Bildkredit: Gurudev Ravindran