Variasjonskoeffisienten er et statistisk mål på fordelingen eller spredningen av data rundt gjennomsnittet. Dette målet brukes til å analysere spredningsforskjellen i dataene i forhold til middelverdien. Variasjonskoeffisient utledes ved å dele standardavviket med gjennomsnittet.
Advarsel
Hvis middelverdien av dataene er null, er det ikke mulig å beregne variasjonskoeffisienten. Tilsvarende, hvis dataene inneholder både positive og negative verdier, er variasjonskoeffisient ikke et pålitelig statisk mål. Variasjonskoeffisient er et pålitelig statisk mål bare hvis dataene inneholder positive verdier.
Tips
Variasjonskoeffisient brukes til å kontrollere konsistensen av data eller prøveverdier i vitenskapelige eksperimenter. Hvis variasjonskoeffisienten er høy, viser den inkonsistensen av data eller prøveverdier.
Trinn 1
Identifiser det settet med tall som variasjonskoeffisienten skal beregnes for. Skriv inn dataene på Excel-arket. Dette eksemplet bruker cellene A2:A7, men Excel-filen din kan bruke andre celler.
Dagens video
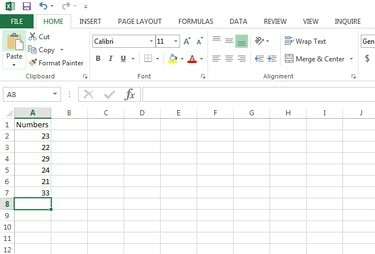
Microsoft Excel dataregistrering.
Bildekreditt: Gurudev Ravindran
Steg 2
Bruk funksjonen Stdev (nummer1, [nummer2]...) å beregne standardavvik i Microsoft Excel. Skriv inn formelen =Stdev (A2:A7) for dette eksemplet -- men skriv inn din faktiske cellebruk i Excel-filen -- i en tom celle og trykk Tast inn for å beregne standardavviket.
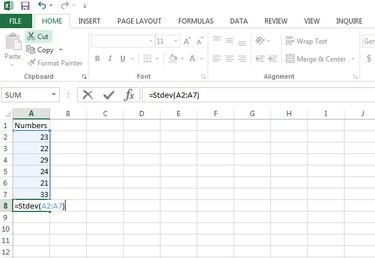
Beregn standardavviket.
Bildekreditt: Gurudev Ravindran
Tips
Hver formel i Microsoft Excel må innledes med likhetstegnet.
Trinn 3
Bruk funksjonen =Gjennomsnitt (tall1, [tall2],...) for å beregne gjennomsnittet i Microsoft Excel.
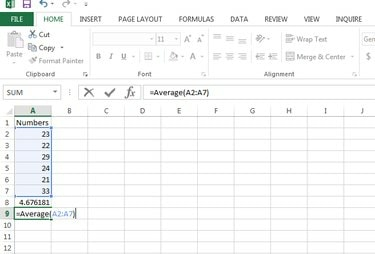
Regn ut gjennomsnittet.
Bildekreditt: Gurudev Ravindran
Trinn 4
For å finne variasjonskoeffisienten, skriv inn formelen =A8/A9 for dette eksemplet eller ditt faktiske område i en tom celle og trykk E**nter** for å beregne variasjonskoeffisienten.
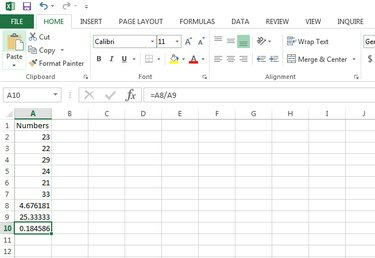
Beregn variasjonskoeffisienten.
Bildekreditt: Gurudev Ravindran


