Voordat u een nieuwe steekproef of populatie van gegevens analyseert, is het handig om elke variabele te onderzoeken individueel om te bepalen of er iets ongewoons is aan de gegevens waar u op moet letten tijdens uw analyse. De functie Beschrijvende statistiek in Excel's Analyse ToolPak berekent een aantal statistieken die u helpen de variabiliteit en centrale tendens van de gegevens te begrijpen.
Stap 1
Afbeelding tegoed: Steve McDonnell/Demand Media
Start Excel. Kiezen Bestand en dan Opties.
Video van de dag
Stap 2
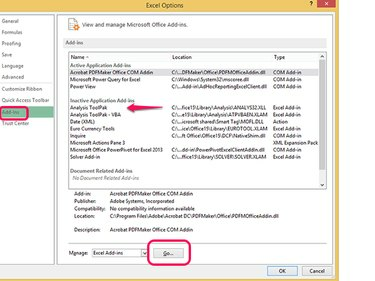
Afbeelding tegoed: Steve McDonnell/Demand Media
Selecteer Invoegtoepassingen uit de lijst met opties in de linkerkolom. Zoek het item Analysis Toolpak in de lijst met invoegtoepassingen aan de rechterkant. Als het niet wordt weergegeven in de lijst met geactiveerde invoegtoepassingen, selecteert u Gaan... om een scherm met invoegtoepassingen te openen.
Stap 3
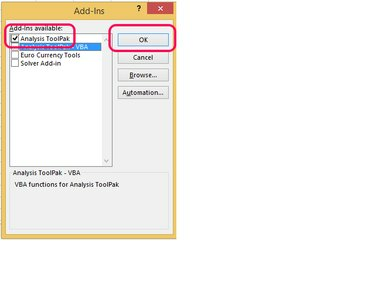
Afbeelding tegoed: Steve McDonnell/Demand Media
Vink het vakje aan naast Analyse ToolPak en kies Oke.
Stap 4

Afbeelding tegoed: Steve McDonnell/Demand Media
Na het activeren van het Analyse ToolPak, of als het al geactiveerd was, kies Oke doorgaan.
Gebruik beschrijvende statistieken
Uw doel bij het gebruik van deze tool is om beschrijvende statistieken te berekenen voor de gegevens die voor een variabele zijn verzameld om die gegevens beter te begrijpen. Een voorbeeld is het analyseren van het aantal seconden dat een racedeelnemer nodig had om één mijl te rennen.
Stap 1

Afbeelding tegoed: Afbeelding met dank aan Microsoft
Open de werkmap die de gegevens bevat die u wilt analyseren: in dit voorbeeld seconden per mijl. Kiezen Gegevens uit de menukaart, Gegevensanalyse van de lintbar, Beschrijvende statistieken uit het vak met selecties en kies vervolgens Oke.
Stap 2
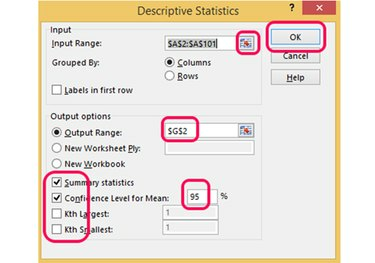
Afbeelding tegoed: Afbeelding met dank aan Microsoft
Typ het celbereik dat de gegevens voor de variabele bevat of klik op de celkiezer knop, markeer het bereik met uw muis en klik nogmaals op de knop. Selecteer een leeg gedeelte van de werkmap om de beschrijvende statistische uitvoer op te slaan en selecteer de soort informatie dat u wilt weergeven, zoals overzichtsstatistieken en 95 procent betrouwbaarheid intervallen. Kiezen Oke om de statistieken te berekenen.
Stap 3
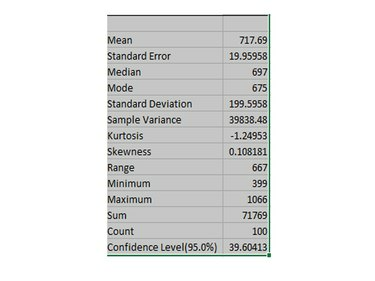
Afbeelding tegoed: Afbeelding met dank aan Microsoft
Gebruik en interpreteer de beschrijvende statistieken als volgt:
-
Gemeen: Gemiddelde waarde - hier zou dat 716,69 seconden zijn, of bijna 12 minuten per mijl.
-
Standaardfout: Dit is hoe dicht uw steekproefwaarden bij het gemiddelde liggen. In een normale verdeling zullen bijna alle waarden binnen drie standaardfouten van het gemiddelde liggen; ongeveer 95 procent zal binnen twee standaardfouten vallen; en ongeveer tweederde zal binnen één standaardfout rond het gemiddelde liggen.
-
Mediaan: Middelste waarde — hier 697 seconden, wat ongeveer 11,6 minuten per mijl is.
-
Modus: Meest gebruikelijke waarde — 675 seconden of 11,25 minuten per mijl.
-
Standaardafwijking: Een indicatie van hoe wijdverbreid de cijfers rond het gemiddelde liggen.
-
Kurtosis: Geeft aan of de gegevens pieken of vlak zijn wanneer ze worden uitgezet in vergelijking met een normale verdeling. De kurtosis voor een normale verdeling is 3.
-
Scheefheid: Geeft aan of de gegevens symmetrisch zijn wanneer ze worden uitgezet in vergelijking met een normale verdeling. De scheefheid voor een normale verdeling is 0.
-
Bereik: Het verschil tussen de laagste en hoogste waarden — 667 seconden of ongeveer 11,1 minuten.
-
Minimum: De laagste waarde in de dataset — 399, wat 6,65 minuten per mijl is.
-
maximaal: De hoogste waarde in de dataset -- 1066 of 17,77 minuten per mijl.
-
Som: De som van alle gegevenspunten.
-
Graaf: Het aantal gegevenspunten.
-
Betrouwbaarheidsniveau (95%): Het interval rond het gemiddelde waarvan u met een kans van 95 procent zeker kunt zijn dat het interval het werkelijke gemiddelde bevat.


