El coeficiente de variación es una medida estadística de la distribución o dispersión de datos alrededor de la media. Esta medida se utiliza para analizar la diferencia de dispersión en los datos en relación con el valor medio. El coeficiente de variación se obtiene dividiendo la desviación estándar por la media.
Advertencia
Si el valor medio de los datos es cero, no es posible calcular el coeficiente de varianza. De manera similar, si los datos contienen valores tanto positivos como negativos, el coeficiente de varianza no es una medida estática confiable. El coeficiente de varianza es una medida estática confiable solo si los datos contienen valores positivos.
Propina
El coeficiente de variación se usa para verificar la consistencia de los datos o valores de muestra en experimentos científicos. Si el valor del coeficiente de variación es alto, representa la inconsistencia de los datos o valores de la muestra.
Paso 1
Identifique el conjunto de números para los que se calculará el coeficiente de variación. Ingrese los datos en la hoja de Excel. Este ejemplo usa celdas A2: A7, pero su archivo de Excel puede usar otras celdas.
Video del día
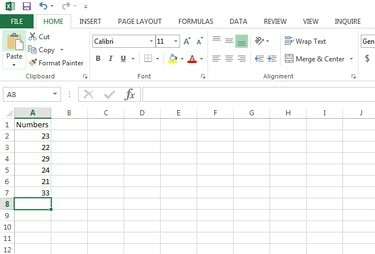
Entrada de datos de Microsoft Excel.
Credito de imagen: Gurudev Ravindran
Paso 2
Usa la función Stdev (número1, [número2],…) para calcular el Desviación Estándar en Microsoft Excel. Ingrese la fórmula = Stdev (A2: A7) para este ejemplo, pero ingrese su uso real de celda en su archivo de Excel, en una celda en blanco y presione Ingresar para calcular la desviación estándar.
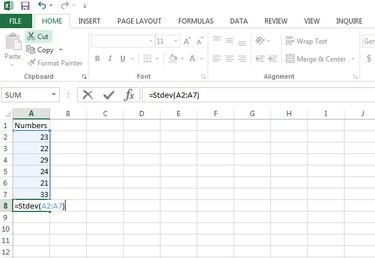
Calcula la desviación estándar.
Credito de imagen: Gurudev Ravindran
Propina
Todas las fórmulas de Microsoft Excel deben ir precedidas del signo igual.
Paso 3
Usa la función = Promedio (número1, [número2],…) para calcular la media en Microsoft Excel.
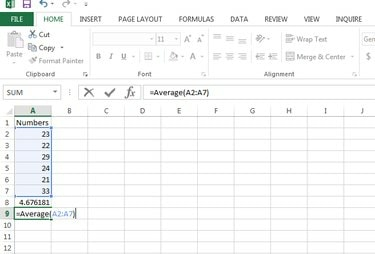
Calcule la media.
Credito de imagen: Gurudev Ravindran
Etapa 4
Para encontrar el coeficiente de variación, ingrese la fórmula = A8 / A9 para este ejemplo o su rango real en una celda en blanco y presione MI**nter ** para calcular el coeficiente de varianza.
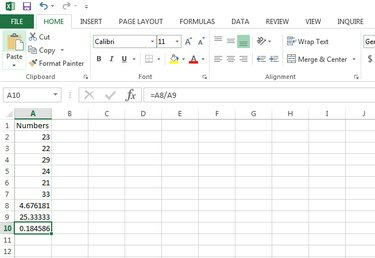
Calcula el coeficiente de varianza.
Credito de imagen: Gurudev Ravindran



