Variationskoefficienten er et statistisk mål for fordelingen eller spredningen af data omkring gennemsnittet. Dette mål bruges til at analysere forskellen i spredningen i dataene i forhold til middelværdien. Variationskoefficienten udledes ved at dividere standardafvigelsen med middelværdien.
Advarsel
Hvis middelværdien af dataene er nul, er det ikke muligt at beregne variansen. Tilsvarende, hvis data indeholder både positive og negative værdier, er varians koefficient ikke et pålideligt statisk mål. Variationskoefficient er kun et pålideligt statisk mål, hvis dataene indeholder positive værdier.
Tip
Variationskoefficient bruges til at kontrollere konsistensen af data eller prøveværdier i videnskabelige eksperimenter. Hvis variationskoefficientværdien er høj, viser den inkonsistensen af data eller stikprøveværdier.
Trin 1
Identificer det sæt af tal, som variationskoefficienten skal beregnes for. Indtast data på Excel-arket. Dette eksempel bruger celler A2:A7, men din Excel-fil kan bruge andre celler.
Dagens video
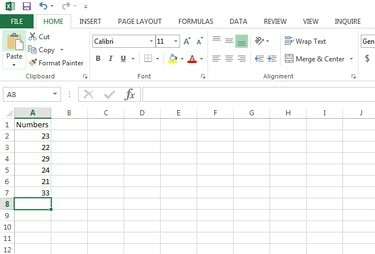
Microsoft Excel dataindtastning.
Billedkredit: Gurudev Ravindran
Trin 2
Brug funktionen Stdev (nummer1, [nummer2]...) at beregne standardafvigelse i Microsoft Excel. Indtast formlen =Stdev (A2:A7) for dette eksempel -- men indtast dit faktiske celleforbrug i din Excel-fil -- i en tom celle og tryk Gå ind at beregne standardafvigelsen.
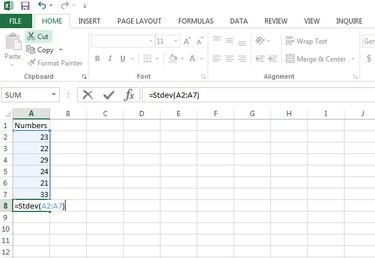
Beregn standardafvigelsen.
Billedkredit: Gurudev Ravindran
Tip
Hver formel i Microsoft Excel skal indledes med lighedstegnet.
Trin 3
Brug funktionen =Gennemsnit (tal1, [tal2],...) for at beregne gennemsnittet i Microsoft Excel.
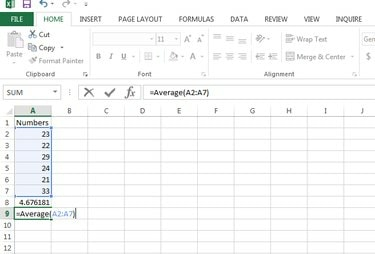
Beregn middelværdien.
Billedkredit: Gurudev Ravindran
Trin 4
Indtast formlen for at finde variationskoefficienten =A8/A9 for dette eksempel eller dit faktiske område i en tom celle, og tryk på E**nter** for at beregne varianskoefficienten.
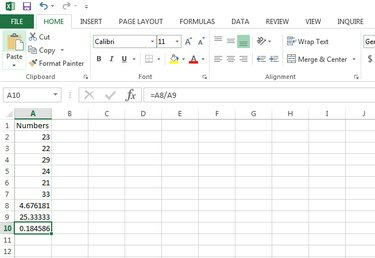
Beregn variationskoefficienten.
Billedkredit: Gurudev Ravindran




